motivation
experience replay是DQN的一个关键技术，它通过存取transition的操作打破了数据之间的相关性，使得数据满足优化方法（e.g., SGD）的假设（i.e., i.i.d.），从而提高了学习的效果。
naive的experience replay在取transition时采用的策略是均匀采样，对所有transition一视同仁。但直觉上来说，各个transition的重要性应该是不同的，有的transition的“信息量”比较大，有的transition则没什么用。
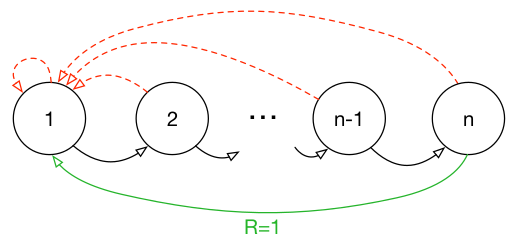
我们拿一个具体的例子来说明均匀采样有什么问题，假设我们有一个如下图所示的environment，它有$n$个状态，$2$个动作，初始状态为$1$，状态转移如箭头所示，当且仅当沿绿色箭头走的时候会有$1$的reward，其余情况的reward均为$0$。那么假如采用随机策略从初始状态开始走$n$步，我们能够获得有用的信息（reward非$0$）的可能性为$1/2^n$。也就是说，假如我们把各transition都存了起来，然后采用均匀采样来取transition，我们仅有$1/2^n$的概率取到有用的信息，这样的话学习效率就会很低。
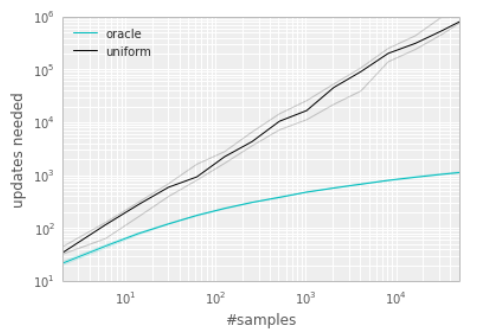
作者还做了个实验，来说明transition的选取顺序对学习效率有很大的影响。下图横轴代表experience replay的大小，纵轴表示学习所需的更新次数。黑色的线表示采用均匀采样得到的结果，绿色的线表示每次都选取”最好“的transition的结果。可以看到，这个效率提升是很明显的。
于是很自然的就会有一个想法，能不能通过优先学习那些“信息量”比较大的transition来提高学习效率呢？
idea
- 首先需要给出一个衡量“信息量”大小的指标，文中用的是TD-error。
- 有了一个评价指标之后，最直接的想法是贪心地选”信息量“最大的transition。但这种贪心的方法有以下问题：
- 贪心的依据不准确：由于考虑到算法效率，我们不会每次critic更新后都更新所有transition的TD-error，我们只会更新当次取到的transition的TD-error。因此transition的TD-error对应的critic是以前的critic（更准确地说，是上次取到该transition时的critic）而不是当前的critic。也就是说某一个transition的TD-error较低，只能够说明它对之前的critic“信息量”不大，而不能说明它对当前的critic“信息量”不大，因此根据TD-error进行贪心有可能会错过对当前critic“信息量”大的transition。
- 容易overfitting：基于贪心的做法还容易“旱的旱死，涝的涝死”（这应该是一个empirical result，因为从原理上来说，被选中的transition的TD-error在critic更新后会下降，然后排到后面去，下一次就不会选中这些transition），来来去去都是那几个transition，导致overfitting。
- 为了处理上述问题，作者提出stochastic prioritization，随机化的采样过程，“信息量”越大，被抽中的概率越大，但即使是“信息量”最大的transition，也不一定会被抽中，仅仅只是被抽中的概率较大。
- 改变采样顺序会改变样本分布，假设原来的样本$x$服从分布$A$，在改变采样顺序后，$x$服从的分布为$B$，我们要求的是$\mathbb{E}_{x \sim A}[f(x)]$，而我们现在只有$\mathbb{E}_{x \sim B}[ \bullet ]$。因此我们需要基于分布$B$的期望来计算在分布$A$下的期望，这就是importance sampling的作用。
detail
- 两种stochastic prioritization方案
- 两种方案都基于以下概率模型（softmax）：
$$
P(i) = \frac{p_i^\alpha}{\sum_k p_k^\alpha},
$$其中$p_i$为第$i$个transition的priority，$\alpha$用于调节优先程度（$\alpha = 0$的时候退化为均匀采样）。而两种方案的区别在于对priority的定义不同。
- proportional prioritization
- $p_i = \vert \delta_i \vert + \epsilon$，其中$\delta_i$为TD-erroe，$\epsilon$用于防止概率为$0$。
- 可能会对outlier更加敏感。
- 实现的时候采用sum tree的数据结构。
- rank-based prioritization
- $p_i = 1/\text{rank}(i)$。
- 只是定性地考虑priority，没有定量地考虑priority。
- 实现类似分层抽样，事先将排名段分为几个等概率区间，再在各个等概率区间里面均匀采样。比如说，假设experience replay大小为100，batch size为3，那么就事先通过计算，将100分为3个等概率区间（e.g., A:1-20，B:21-50, C:51-100），之后就在A、B和C区间内分别做均匀采样，最后取得3个transition。
- 两种方案都基于以下概率模型（softmax）：
- importance sampling
- 核心公式为：
$$\mathbb{E}_{x \sim A}[f(x)] = \sum_x P_A(x)f(x) = \sum_x P_B(x) \frac{P_A(x)}{P_B(x)}f(x) = \mathbb{E}_{x \sim B}[\frac{P_A(x)}{P_B(x)}f(x)].$$ - 将具体的$P_A(x)=1/N$与$P_B(x)=P(i)$代入后，就得到所谓的importance-sampling weight
$$
w_i = (\frac{1}{N} \cdot \frac{1}{P(i)})^\beta,
$$其中，$\beta$用于调节bias程度（作者argue说学习的初始阶段有bias也没所谓，但在后期就要消除bias）。 - 作者还说这个importance sampling要除以$\text{max}_i w_i$（这个$i$应该是指minibatch，如果是指experience replay的话，那在采取proportional prioritization的时候开销就太大了），以此保证update一定是scale downward的（感觉是为了控制step size）。
- 核心公式为：
more
- 针对具体问题，某种stochastic prioritization方案会表现得比另外一种更好。
- 类似的priority思想可以用到supervised learning中。
- 某个transition被访问的次数反映了这个transition的“重要性”，可以作为一个feedback signal给到exploration。
- 可以通过这种方法减小experience replay的大小，从而减少训练所需的内存。